Matematiikalla on ratkaiseva rooli käyttäytymisen ja toiminnan ymmärtämisessä sähköinen ja elektroniset järjestelmät . Polynomit, algebra, todennäköisyys, integraatiot ja erottelut jne.… Muodostavat merkittävän osan työkaluista, joita käytetään järjestelmien ratkaisemiseen. Järjestelmien monimutkaisuuden myötä tarvitaan erittäin kehittyneitä menetelmiä. Differential yhtälöitä käytetään näkyvästi ohjausjärjestelmien määrittelyssä. Nämä yhtälöt on helppo ratkaista. Mutta monimutkaisuus syntyy ratkaistaessa korkeamman asteen differentiaaliyhtälöitä. Tällaisten monimutkaisten korkeamman asteen differentiaaliyhtälöiden ratkaisemiseksi matemaattinen menetelmä, joka osoittautui tehokkaaksi, on Laplace-muunnos . Koska tätä muutosta käytetään laajalti, on hyödyllistä tietää, mihin he todella tarkoittivat ja miten ne toimivat.
Mikä on Laplace-muunnos?
Matematiikassa käytetään muunnoksia muuttujan muuntamiseksi muodosta toiseen, jotta yhtälö olisi helppo käsitellä. Laplace-muunnokset tekevät melkein saman. Ne muuttavat korkeamman kertaluvun differentiaaliyhtälön polynomimuodoksi, joka on paljon helppoa kuin differentiaaliyhtälön ratkaiseminen suoraan.
Mutta on olemassa erilaisia muunnoksia, kuten Fourier-muunnos, z muuttaa, mikä tekee Laplace-muunnoksesta erityisen? Laplace-muunnoksen suurin etu on, että ne on määritelty sekä vakaille että epävakaille järjestelmille, kun taas Fourier-muunnokset on määritelty vain vakaille järjestelmille.
Laplace-muunnoskaava
Funktion f (t) Laplace-muunnos aikatasossa, jossa t on todellinen luku suurempi tai yhtä suuri kuin nolla, annetaan muodossa F (s), missä  s on taajuusalueen kompleksiluku. s = σ + jω
s on taajuusalueen kompleksiluku. s = σ + jω
Yllä olevaa yhtälöä pidetään yksipuolinen Laplace-muunnosyhtälö . Kun rajat ulotetaan koko todelliseen akseliin, niin Kahdenvälinen Laplace-muunnos voidaan määritellä
 Käytännön piireissä, kuten RC- ja RL-piirit yleensä käytetään alkuolosuhteita, joten yksipuolisia Laplace-muunnoksia käytetään analyysitarkoituksiin.
Käytännön piireissä, kuten RC- ja RL-piirit yleensä käytetään alkuolosuhteita, joten yksipuolisia Laplace-muunnoksia käytetään analyysitarkoituksiin.
Koska s = σ + jω, kun σ = 0, Laplace-muunnokset käyttäytyvät Fourier-muunnoksina.

Laplace-muunnoskaavat
Laplace-muunnoksen soveltamisedellytykset
Laplace-muunnoksia kutsutaan integraaleiksi muunnoksiksi, joten näiden muunnosten lähentymiselle on välttämättömät ehdot.
 ts. f: n on oltava paikallisesti integroitavissa aikavälillä [0, ∞) ja riippuen siitä, onko σ positiivinen vai negatiivinen, e ^ (- σt) voi olla hajoamassa tai kasvamassa. Kahdenvälisissä Laplace-muunnoksissa yhden arvon sijasta integraali lähenee tietyn arvon alueen, joka tunnetaan nimellä lähentymisalue.
ts. f: n on oltava paikallisesti integroitavissa aikavälillä [0, ∞) ja riippuen siitä, onko σ positiivinen vai negatiivinen, e ^ (- σt) voi olla hajoamassa tai kasvamassa. Kahdenvälisissä Laplace-muunnoksissa yhden arvon sijasta integraali lähenee tietyn arvon alueen, joka tunnetaan nimellä lähentymisalue.
Laplace-muunnoksen ominaisuudet:
Lineaarisuus

Lineaarisuus
Ajansiirto

Ajansiirto
Vaihto S-verkkotunnuksessa

Vaihto S-verkkotunnuksessa
Ajan kääntäminen

Ajan kääntäminen
Eriyttäminen S-verkkotunnuksessa

Eriyttäminen S-verkkotunnuksessa
Konvoluutio ajassa

Konvoluutio ajassa
Alkuarvolause
Alkuarvolause käytetään, kun Laplace-muunnoksessa osoittajan aste on pienempi kuin nimittäjän aste  Lopullisen arvon lause:
Lopullisen arvon lause:
Jos kaikki sF: n (t) napat ovat S-tason lopullisen arvon lauseen vasemmalla puoliskolla.
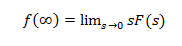 Käänteinen Laplace-muunnos
Käänteinen Laplace-muunnos
Lähentymisen vuoksi Laplace-muunnoksella on myös käänteinen muunnos. Laplace-muunnoksissa on yksi kerrallaan kartoitus funktiotilasta toiseen. Käänteisen Laplace-muunnoksen kaava on
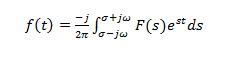 Kuinka laskea Laplace-muunnos?
Kuinka laskea Laplace-muunnos?
Laplace-muunnos tekee yhtälöistä yksinkertaisempia käsitellä. Kun annetaan korkeamman asteen differentiaaliyhtälö, siihen sovelletaan Laplace-muunnosta, joka muuntaa yhtälön algebralliseksi yhtälöksi, mikä helpottaa sen käsittelyä. Sitten laskemme juuret yksinkertaistamalla tätä algebrallista yhtälöä. Nyt löydetään yksinkertaisemman lausekkeen käänteinen Laplace-muunnos, joka ratkaisee annetun korkeamman asteen differentiaaliyhtälön.

Laplace-muunnoksen laskenta
Laplace Transform -sovellukset
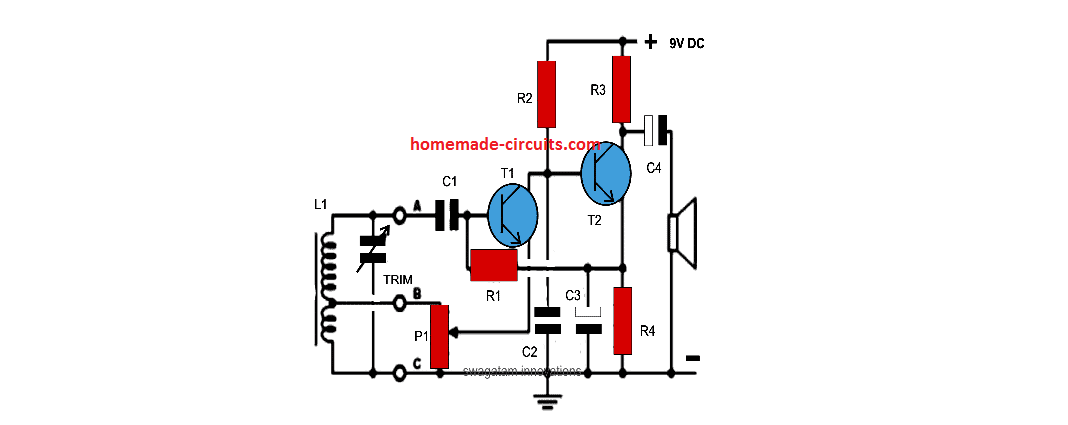
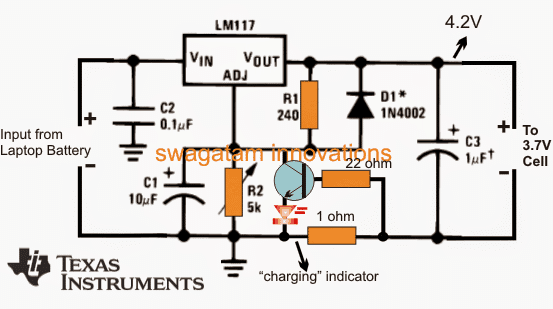
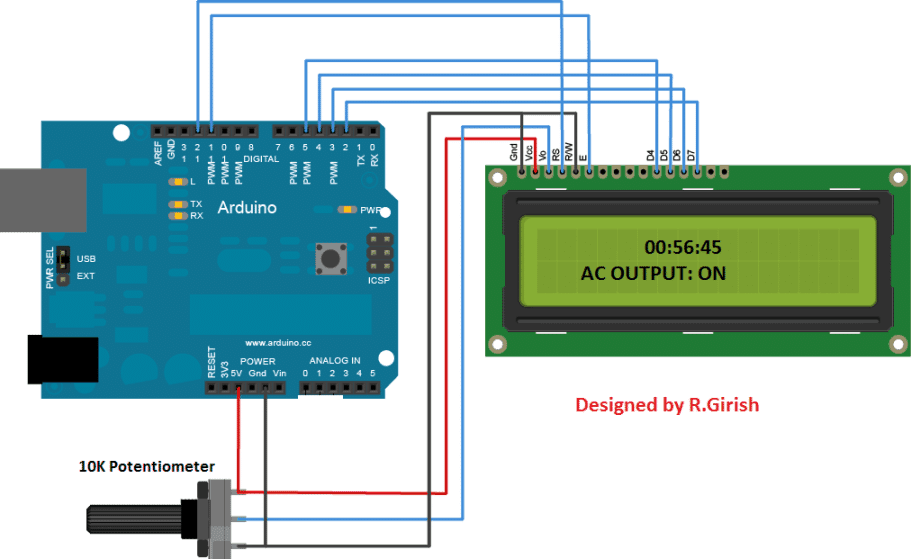
- Analyysi sähkö - ja elektroniset piirit .
- Jaetaan monimutkaiset differentiaaliyhtälöt yksinkertaisempiin polynomimuotoihin.
- Laplace-muunnos antaa tietoa sekä vakaista että ohimenevistä tiloista.
- Koneoppimisessa Laplace-muunnosta käytetään ennusteiden tekemiseen ja analyysien tekemiseen tiedonlouhinnassa.
- Laplace-muunnos yksinkertaistaa laskelmia järjestelmämallinnuksessa.
Laplace Transform -sovelluksen käyttö signaalinkäsittelyssä
Laplace-muunnokset valitaan usein signaalinkäsittelyä varten. Fourier-muunnoksen ohella Laplace-muunnos käytetään signaalien tutkimiseen taajuusalueella. Kun taajuusalueen signaalissa on pieniä taajuuksia, voidaan odottaa signaalin olevan tasainen aikatasossa. Signaalin suodatus tapahtuu yleensä taajuusalueella, jolle Laplace toimii tärkeänä työkaluna signaalin muuntamiseksi aikatoiminnosta taajuusalueeksi.
Laplace-muunnoksen käyttö ohjausjärjestelmissä
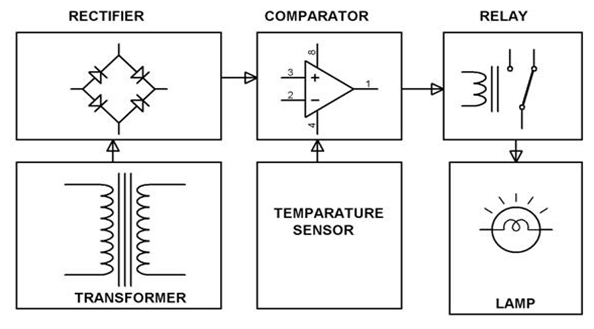
Ohjausjärjestelmät on yleensä suunniteltu ohjaamaan muiden laitteiden toimintaa. Esimerkki ohjausjärjestelmät voi vaihdella yksinkertaisesta kodin lämmitysohjaimesta teolliseen ohjausjärjestelmään, joka säätelee koneiden käyttäytymistä.
Yleensä ohjausinsinöörit käyttävät differentiaaliyhtälöitä kuvaamaan eri suljettujen silmukoiden toiminnallisten lohkojen käyttäytymistä. Laplace-muunnosta käytetään tässä ratkaisemaan nämä yhtälöt menettämättä tärkeitä muuttujatietoja.
Lineaaristen aika-muuttamattomien järjestelmien karakterisointi käyttäen Laplace-muunnosta
Järjestelmään liittyvän rennon järjestelmän ROC: n tapauksessa toiminto on oikea puolitaso. Järjestelmä on rento, jos sen impulssivaste h (t) = 0, kun t> 0.
Jos järjestelmän toimintojen ROC H (s) sisältää jω-akselin, niin L.T.I. järjestelmää kutsutaan stabiiliksi järjestelmäksi. Jos rennolla järjestelmällä, jolla on rationaaliset järjestelmätoiminnot H (s), on negatiivisia reaaliosia kaikille napoilleen, järjestelmä on vakaa.
Siten Laplace-muunnos on ratkaiseva työkalu piirien analysoinnissa. Voimme sanoa, että stetoskooppi on lääkärille, että Laplace-muunnokset ohjaavat insinööriä. Miksi pidät Laplace-muunnoksia? Millä tavalla ne olivat hyödyllisiä sinulle?
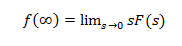 Käänteinen Laplace-muunnos
Käänteinen Laplace-muunnos 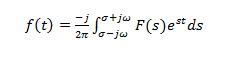 Kuinka laskea Laplace-muunnos?
Kuinka laskea Laplace-muunnos?